2022-12-26 11:24:01 辽宁华图公考问答 http://ln.huatu.com/wenda/ 文章来源:四川华图
本溪华图_本溪公务员招聘考试网。更多招聘信息敬请关注本溪华图教育官网(http://benxi.huatu.com/)或者关注本溪华图微信公众号(bxhtjy),本溪华图咨询电话:024-42825777。
对于给定的平面几何图形,如果已知起点和终点,按照指定的规则,求不同路径的数量。一般通用的方式是逐点标数(本质为递推和数列)。具体方法:①确定起点和终点,在起点处标1;②确定运动方向(转化成上下左右)后转换角度,即每一点可能来的路径数;③由起点到终点(由近及远)逐级求和,每一个点的路径数等于可能到达它的点的路径数之和。理论比较抽象,我们通过几道例题一起来看一下:
【例1】小张从华兴园到软件公司上班要经过多条街道(软件公司在华兴园的东北方)。假如他只能向东或者向北行走,则他上班不同走法共有:
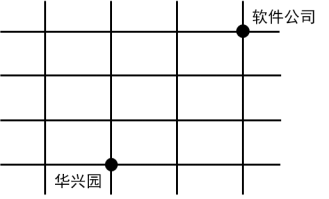
A.12种
B.15种
C.20种
D.10种
【答案】D
【解析】
第一步,已知了起点和终点,并确定了向东和向北的运动方向,求不同走法的总数,采用逐点标数法。先在起点处标1,并在正东和正北方向标1,如下图:
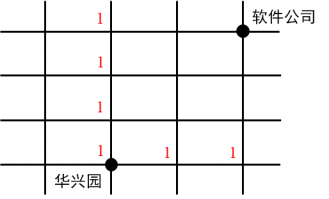
第二步,除起点外,任何一点只能从它的左边和下边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:

因此,选择D选项。
【例2】小赵从家出发去单位上班要经过多条街道(如图),假如他只能向西或向南行走。则他上班有多少种不同的走法?
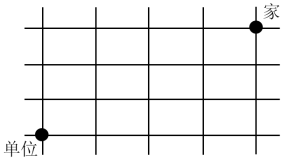
A.6
B.24
C.32
D.35
【答案】D
【解析】
第一步,已知了起点和终点,并确定了向西和向南的运动方向,求不同走法的总数,采用逐点标数法。先在起点处标1,并在正西和正南方向标1,如下图:
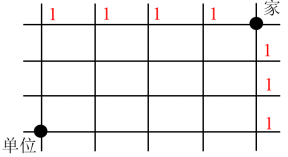
第二步,除起点外,任何一点只能从它的上边和右边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:

因此,选择D选项。
除了标数法之外,还有部分同学会想到用排列组合的方式来求解。如例1种根据“从华兴园到软件公司上班只能向东或者向北行走,至少要走过两条横向马路,三条纵向马路,共5段路”,只要从5段路中,选择2段路走横向即可,故共种。同理,例2也可以使用排列组合的方式,即四条横向道路,三条纵向道路,共7段路,只需要从7段路中,选择3段路走纵向即可,共种。但此类方式有其局限性,并不是通用的解法,如下面的例题使用排列组合的方式会比较困难,而标数法却比较简单。
【例3】从A地到B地的道路如图所示,所有转弯均为直角,问如果要以最短距离从A地到达B地,有多少种不同的走法可以选择?
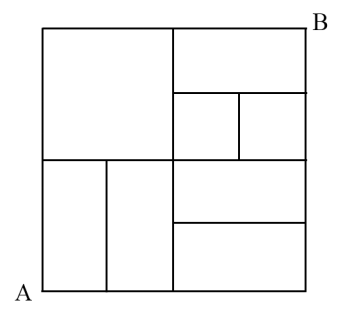
A.14
B.15
C.18
D.21
【答案】B
【解析】
第一步,已知了起点和终点,题干要求最短距离只能向右或向上行进,求不同走法的总数,采用逐点标数法。先在起点A处标1,并在正东和正北方向标1,如下图:
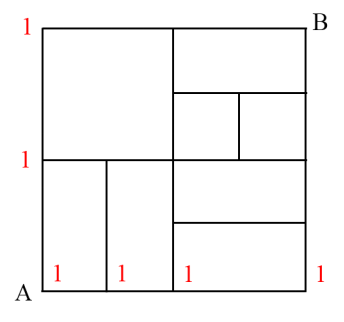
第二步,除起点外,任何一点只能从它的左边和下边过来(因为要求路程最短),分析之后,接着可以标记余下点的路径数。如下图:

因此,选择B选项。
【例4】A、B、C三地的地图如下图所示,其中A在C正北,B在C正东,连线处为道路。如要从A地到达B地,且途中只能向南、东和东南方向行进,有多少种不同的走法:
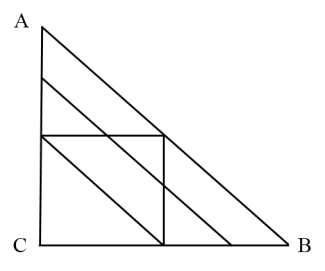
A.9
B.11
C.13
D.15
【答案】D
【解析】
第一步,已知了起点A和终点B,题干要求最短距离只能向南、向东或东南行进,求不同走法的总数,采用逐点标数法。先在起点A处标1,并在正南方向标1,如下图:

第二步,任何一点只能从它的上边、左边和左上方向过来(因为要求路程最短),分析明白之后,接着可以标记余下点的路径数。如下图:
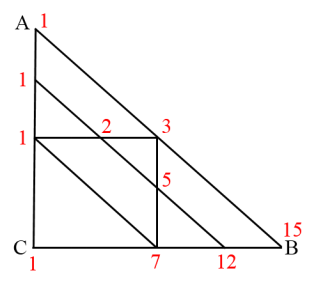
因此,选择D选项。
对于平面几何中的路径类问题,即给定一个平面几何图形,已知起点和终点,按照指定的规则,求不同路径的数量的题目,虽然针对部分简单图形,排列组合可以使用,但并不是最常用的解法,我们最常用的解法是标数法(本质为递推和数列)。当然,需要各位同学把握好题目特征以及具体方法的操作步骤,只有熟练掌握才能灵活自如地运用。
(编辑:本溪华图01)

贴心微信客服

贴心QQ客服
下一篇:没有了