2020-04-12 11:34:07 辽宁华图公考问答 http://ln.huatu.com/wenda/ 文章来源:本溪华图
本溪华图_本溪公务员考试网为您提供辽宁公务员考试热点。更多公务员招聘信息敬请关注本溪华图公务员招聘频道(http://benxi.huatu.com/gwy/)或者关注本溪华图微信公众号(bxhtjy),本溪华图咨询电话:024-42825777。
涉及到因式分解、不等式、函数图像等考点,所涉及的考点整体考查的计算难度不高,但对题目分析能力要求较高。
一些公式要牢记:

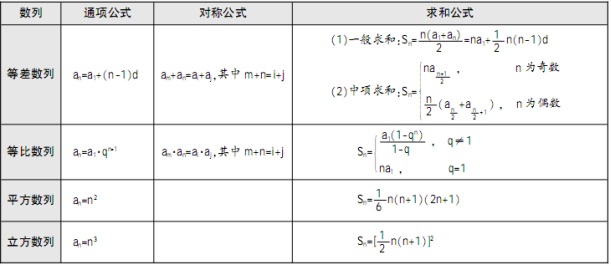
记住了没?来考考大家。
【例题一】计算:1005×10061006-1006×10051005=( )
A.0 B.100 C.1000 D.10000
【解析】A。
发现10061006和10051005结构比较相似,可采用提取公因式10001的方式。原式=1005×1006×10001-1006×1005×10001=0。因此A项当选。
【例题二】某制衣工厂对9名工人进行技术评比,9名工人的得分恰好成等差数列、9人的平均得分是86分,前5名工人的得分之和是460分,那么前7名工人的得分之和是多少?
A.602 B.623 C.627 D.631
【解析】B。
9人得分成等差数列,故9人的平均数应为第五名的成绩86分。前5名得分之和为460分,平均分为460÷5=92分,因此第4名的得分为(86+92)÷2=89分,所以前7名工人的得分为89×7=623分。
涵盖了利润、成本、售价几个基本量的考点,考察内容主要以简单计算和公式的应用为主,在计算上技巧性不强,主要考察计算能力,以解方程为主。
这些基本公式要熟悉:
公式1、利润=售价-成本=成本×利润率
公式2、利润率=(利润÷成本)×100%=售价÷成本-1
公式3、售价=成本+利润=成本×(1+利润率)
公式4、打折率=售价÷定价=(1+折后利润率)÷(1+折前利润率)
但是有些题目直接套用公式是不行的,还需要掌握一些方法。我们一起看看解决利润问题的常用方法之方程法。
【例题一】某商场采购一种电冰箱,先按进价15%的利润定价,此后按定价的90%出售,结果每台盈利210元,问这种冰箱的进价是多少元?
A.6000元 B.5000 C.4000 D.3000
【解析】A。
这道题目首先关注问法,求的是进价也就是成本。不防我们把成本设为X,如果采用方程法去解题除了设未知数还要找等量关系列出方程。我们不难发现利润=售价-成本,带入公式,1.15X×0.9-X = 210。解出X=6000。答案选择A选项。
这就是基本方程法的应用,为什么这道题目我们设成本为X呢。同学们不防去思考一下。其实一方面是因为这道题目问的是成本。另一方面我们在设出成本的时候,这时候售价就可以通过利润率快速表示。所以我们设成本会简单一些。
涉及到基本的排列数和分步分类思想,考查计算难度不大,但较难分析。犀鸟公考给大家推荐以下三种常见的解题方法:
1. 优先法:有特殊要求的元素优先考虑。
【例题一】某大学考场在8个时间段内共安排了10场考试,除了中间某个时间段(非头尾时间段)不安排考试外,其他每个时间段安排1场或2场考试。那么,该考场有多少种考试安排方式(不考虑考试科目的不同)?
A.210 B.270 C.280 D.300
【解析】A。
第一步,要求中间某个时间段不安排考试,说明要从6个时间段中选一个共6,第二步,安排一场或者两场,剩下的7个时间段最少要有一场,还剩3场,所以从剩下的7个时间段,选3个,就可以,因为不考虑科目,为组合,共有35种,第三步,分步用乘法6*35=210,答案A。
2. 捆绑法:相邻问题捆绑法(将相邻元素看成大元素,再考虑内部情况
【例题二】四对情侣排成一队买演唱会门票,已知每对情侣必须排在一起,问共有多少种不同的排队顺序?
A.24 种 B.96 种 C.384 种 D.40320 种
【解析】C。
每对在一起,说明要捆绑,将这4对,看成4个大元素,排列共有4*3*2*1=24,在考虑内部情况没对都有两种,共24*2*2*2*2=384,答案C。
3. 插空法:不相邻问题插空法(先将不相邻元素不看,再将不相邻元素插入空中
【例题三】某市至旱季水源不足,自来水公司计划在下周七天内选择两天停止供水,若要求停水的两天不相连,则自来水公司共有()种停水方案。
A.21 B.19 C.15 D.6
【解析】C。
要求不相邻,要使停水的两天不相连,就相当于把停水的 2 天插入不停水 的 5 天所形成的 6 个空位中,有 6个空中选2个(无序) 共15 种停水方案。
涉及到了平面几何问题以及三角函数,平面几何问题一直以来都是几何问题的重要考点。三角函数出现的比较少,一旦出现,三角函数就是拉开分差的题目。
犀鸟公考总结了常用的集合图形的公式:
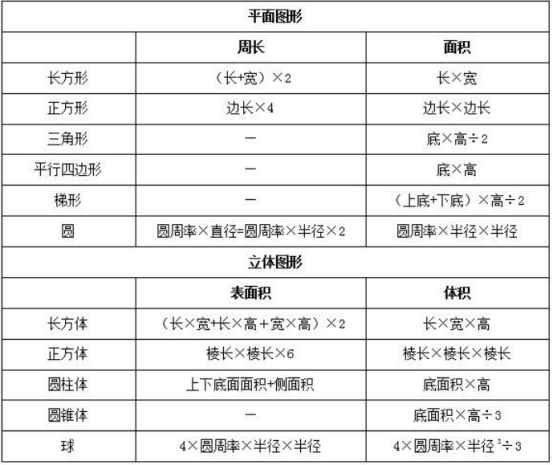
【例题一】一个长方体模型,所有棱长之和为72,长、宽、高的比是4∶3∶2,则体积是多少?
A.72 B.192 C.128 D.96
【解析】B。
所有棱长(长、宽、高各4条)之和为72,即长+宽+高=72÷4=18,已知长、宽、高的比是4∶3∶2,所以长为8、宽为6、高为4,体积=8×6×4=192。
【例题二】一个长方体形状的盒子长、宽、高分别为20厘米、8厘米和2厘米,现在要用一张纸将其六个面完全包裹起来,要求从纸上剪下的部分不得用作贴补,请问这张纸的大小可能是下列哪一个?
A.长25厘米、宽17厘米 B.长26厘米、宽14厘米
C.长24厘米、宽21厘米 D.长24厘米、宽14厘米
【解析】C。
该长方体的表面积为2×(20×8+20×2+8×2)=432平方厘米,这张纸的面积一定要大于长方体的表面积,选项中只有C项符合。
主要包括基本工程、多者合作、交替合作等题型。基本工程问题难度不高,抓住工程问题所涉及的公式和正反比关系就能够解决绝大部分提醒。
①基本公式:总工作量=工作时间×工作效率
②正反比关系:工作时间一定时,工作效率与总工作量成正比
工作效率一定时,工作时间与总工作量成正比
总工作量一定时,工作时间与工作效率成反比
(一)已知多个完成工作的时间,设工程总量为多个时间的最小公倍数,进而求出工作效率
【例题一】A、B、C、D四个工程队修建一条马路,A、B合作可用8天完成,A、C或B、D合作可用7天完成,问C、D合作能比A、B合作提前几天完成?
A.16/9 B.15/8 C.7/4 D.2
【解析】A。
题干给出AB合作8天完成,求出CD合作的天数可得出答案。结合题干信息,给出多个完成工作的时间,设工程总量为其最小公倍数56。根据工作效率等于工作总量和工作时间之比,可得AB的合效率为7,AC和BD的合效率都为8。抓住目标,所求CD合作完成工作时间,需求CD的效率。分析前面各效率之间的关系,CD的效率=AC+BD-AB=8+8-7=9,可得CD合作所需天数为56÷9=56/9。所以比AB合作提前8-56/9=16/9,选A。
(二)已知每人/物工作效率相同,设每人/物工作效率为单位1,进而求出工程总量
【例题二】建筑公司安排100名工人修路,每名工人的修路速度一样。工作两天后调走30名工人,又工作了5天后再抽调走20名工人,总共用时12天完成。如果希望整条路10天修完,且中途不得增减人手,则需要安排多少名工人?
A.80 B.90 C.100 D.120
【解析】A。
题干给出每名工人的工作效率相同,直接设每人的工作效率为“1”。根据工作总量等于工作效率和工作时间之积。工作前2天100名工人,工作效率为100,前2天工作总量为100×2=200;工作中间5天剩70名工人,工作效率为70,中间5天工程总量为70×5=350;最后工作5天剩50名工人,工作效率为50,最后5天工程总量为50×5=250。可得12天的工作总量为200+350+250=800。题干要求10天修完,每天所需工作效率为800÷10=80,即需要80名工人,选A。
涉及的类别很多,比如说普通行程、相遇追及、多次相遇、牛吃草、流水行船等等问题,很多考生遇到了都感到有点无从下手。
解决这类问题,最主要运用两种方法:一个是公式法,一个是正反比思想。
①公式法:S=V*T
②正反比思想:运用比例的转换思想。当路程S一定,V和T成反比;当速度V一定,S和T成正比;当时间T一定,S和V成正比。
下面尝试用这两种方法解题:
【例题一】一列长 90 米的火车以每秒 30 米的速度匀速通过一座长 1200 米的桥,所需时间为( )。
A.37 秒 B.40 秒 C.43 秒 D.46 秒
【解析】C。
解析:需要注意火车自身有长度,需要加在路程中进行计算。火车走过的路程为 1200+90=1290 米,因此所需时间为t=s/v=1290÷30=43 秒。
【例题二】小张准备骑自行车到 A 地出席同学 12 点举行的聚会,出发时计划了一下,慢速 骑车每小时走 6 千米,迟到 2 小时,快速骑车每小时走 12 千米,早到 2 小时。若小张 12 点准时到达,则每小时需骑( )千米。
A.7 B.8 C.9 D.10
【解析】B。
①设小张准点参加聚会需要走 x 小时,则第一种情况可以列式为:s= 6(x+2)。第二种情况列式为:是s=12(x-2)。联立两式子得到:6(x+2)=12(x-2)。解得 x=6。总路程为S= 6×(6+2)=48 千米,要准点到达,每小时需骑 48÷6=8 千米。
②通过正反比解题,可以发现路程S一定,V和T应该成反比,已知速度比为6:12=1:2,时间比应该是2:1。根据题干分析一个迟到2小时,一个早到2小时,可见时间差为4h,1份代表4h,得出第一种情况为8h,实际准时时间为8-2=6h,速度为6*8/6=8千米每小时。
(编辑:本溪华图01)

贴心微信客服

贴心QQ客服